Cubemap Rendering Sample

Overview

This sample demonstrates various cubemap rendering techniques, including ones that use the Multi-Projection Acceleration feature introduced in Maxwell GM20x.

A cubemap has 6 faces that correspond to 6 different projections of the same scene onto faces of a cube. In order to render a cubemap, one has to draw each triangle one or multiple times. There are some well-known approaches to render a cubemap:

1. Render each cube face separately, using the standard rendering pipeline, drawing every mesh multiple times and changing the view/projection matrices according to the face being drawn. In order to improve performance, per-mesh culling can be applied, i.e. there is no need to draw a mesh for a certain face if it can be determined that no part of that mesh will project onto that face.
2. Render all faces at once using a geometry shader to compute multiple projections of each triangle and render the triangle into multiple faces. Per-mesh culling can also be applied here by computing a mask of faces that a mesh may project onto and passing that mask to the geometry shader through a uniform value. Finer-grained culling can be performed by analyzing each triangle in the GS and determining the set of cube faces per triangle.

This sample introduces two important techniques that significantly improve performance of cubemap rendering.

Cubemap rendering with Multi-Projection Acceleration

The MPA feature consists of three sub-features:

1. Pass-through Geometry Shader, or Fast GS, described in the GL_NV_geometry_shader_passthrough extension. This is a lightweight GS that cannot write any per-vertex attributes, but it can read and analyze those attributes, and it can create per-primitive attributes.
2. Viewport multicast, described in the same extension. This feature allows one primitive to be rasterized into several viewports and render target layers at once, without the need to replicate the primitive in the geometry shader or anywhere else.
3. Viewport swizzle, described in the GL_NV_viewport_array2 extension. This feature allows vertex coordinates to be transformed just before rasterization; the transformation is limited to coordinate swizzle and sign changes, and it is defined independently for each viewport.

Using viewport multicast and swizzle and the fact that the cube map projections are highly symmetric, we can construct a rendering algorithm that processes every triangle once and uses a very simple geometry shader.

When the scene geometry is properly transformed (translated, rotated and scaled) in the vertex shader, the cube map faces become aligned parallel to the major planes (XY, XZ, YZ) and cross the X, Y, Z axes at –1 or 1. Correspondingly, the projection frusta are also aligned along the major axes and have common top/bottom/left/right planes. In this case, transforming a vertex from cube-local coordinates to view space can be performed with rotation only. More importantly, this rotation is always a multiple of 90 degrees, so all the members of the rotation matrix are 0, 1 or –1, and each component of the result vector only depends on one component of the source vector. Such matrix can be replaced with simple swizzling of coordinates. Transforming the view space coordinates to clip space using swizzling is trickier because usually clip-space Z is a linear function of view-space Z, so that post-projection Z/W is within range (0, 1) where 0 is the near plane and 1 is the far plane. We cannot compute a linear function with coordinate swizzle, but there is still a way: we can make clip-space Z = 1 and clip-space W = view Z. This way, Z/W = 0 means the far plane at infinity, and Z/W = 1 means the near plane at 1.

Viewport swizzle state is set from the CPU using the glViewportSwizzleNV function; refer to the sample source code for actual usage and swizzle pattern encodings. The geometry shader that is required for this algorithm to work is trivial and mostly declarative:

#extension GL_EXT_geometry_shader4 : enable
#extension GL_NV_viewport_array2 : enable
#extension GL_NV_geometry_shader_passthrough : require

layout(triangles) in;
layout(passthrough) in gl_PerVertex {
    vec4 gl_Position;
};

layout(viewport_relative) out int gl_Layer;

void main()
{
    gl_ViewportMask[0] = 0x3f;
}

Fast Cubemap Culling Algorithm

This section describes an efficient algorithm to conservatively compute the set of cube map faces that a given triangle may be rasterized into. This algorithm can be implemented with only a few instructions in both vertex and geometry shaders.

The idea

The main idea is that a triangle will not project onto the given face if all its vertices are located at the wrong side of any of the planes forming the face?s frustum.

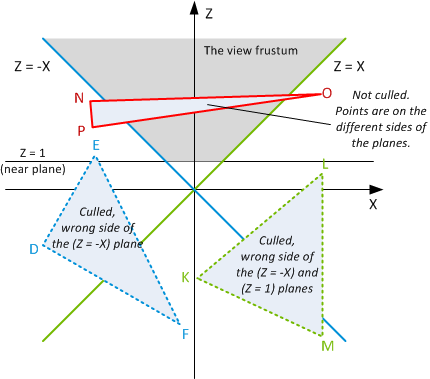
Figure 1: Culling planes projected onto the XZ plane

In a 2D case shown on Fig. 1, a triangle ABC is culled, i.e. not drawn, if:

    ((A.z < A.x)  && (B.z < B.x)  && (C.z < C.x))   // plane Z = X
||  ((A.z < -A.x) && (B.z < -B.x) && (C.z < -C.x))  // plane Z = -X
||  ((A.z < 1)    && (B.z < 1)    && (C.z < 1))     // plane Z = 1

For example, triangle DEF on Fig. 1 is culled because all its vertices are on the wrong side of the Z = –X plane (second line of the condition). Triangle KLM is culled because of the planes Z = X and Z = 1, and triangle NOP is not culled because there is no plane that leaves all three vertices in the culled half space.

Evaluating similar expressions for all 6 cube map faces will give us 6 flags that indicate the faces which do not contain any part of the triangle. The inverse of these flags therefore makes the mask of the viewports into which the triangle should be rasterized.

The implementation

Let?s ignore the near clip planes (Z = 1) for now.

There are only 6 different planes that create all 6 frusta (pyramids if we omit the near planes): X = Y, X = –Y, X = Z, X = –Z, Y = Z, Y = –Z. This means that we can compute 6 flags for each vertex, and these flags will describe the side of that vertex relative to each plane, i.e. which half space defined by this plane does each vertex belong to. Then we combine these flags using logical expressions to compute the viewport mask.

Since the flags are computed independently for each vertex, we can compute them in the vertex shader (or the domain shader in case tessellation is being used) and pass them to the geometry shader. Here?s the vertex shader code, excluding the model-view transformations:

out float planeMask;

int getVertexPlaneMask(vec3 v)
{ 
    return int(v.x < v.y) | 
        (int(v.x < -v.y) << 1) | 
        (int(v.x <  v.z) << 2) | 
        (int(v.x < -v.z) << 3) | 
        (int(v.z <  v.y) << 4) | 
        (int(v.z < -v.y) << 5);
}

void main(void) {
    gl_Position = gl_Vertex;
    planeMask = float(getVertexPlaneMask(gl_Vertex.xyz));
}

The output attribute ?planeMask? of the vertex shader is a bit field with 6 bits where each bit encodes the relation of the vertex processed by this vertex shader instance and one of the 6 planes.

The geometry shader first gets the three plane masks computed by the vertex shader "pm0".."pm2", and then it computes all-vertex predicate masks:

in float planeMask[];
void main() {
    int pm0 = int(PlaneMask[0]);
    int pm1 = int(PlaneMask[1]);
    int pm2 = int(PlaneMask[2]);
    int prim_plane_mask_0 = pm0 & pm1 & pm2;
    int prim_plane_mask_1 = ~pm0 & ~pm1 & ~pm2;

Each bit of ?prim_plane_mask_0? encodes the condition that all vertices are in one half space of the corresponding plane. Each bit of ?prim_plane_mask_1? encodes that all vertices are the other half space.

Then the geometry shader combines these masks into one word and computes the 6 predicates for cube map faces. The predicates are then combined into one viewport mask and passed to the rasterization pipeline.

    int combined_mask = prim_plane_mask_0 | (prim_plane_mask_1 << 8);
    int xp = (combined_mask & 0x000f) == 0 ? 0x01 : 0;
    int xn = (combined_mask & 0x0f00) == 0 ? 0x02 : 0;
    int yp = (combined_mask & 0x1122) == 0 ? 0x04 : 0;
    int yn = (combined_mask & 0x2211) == 0 ? 0x08 : 0;
    int zp = (combined_mask & 0x0438) == 0 ? 0x10 : 0;
    int zn = (combined_mask & 0x3804) == 0 ? 0x20 : 0;
    gl_ViewportMask[0] = xp | yp | zp | xn | yn | zn;
}

These magic numbers require some explanation. First, let?s write down the full culling expressions for all 6 cube map faces.

    Does NOT project to +X viewport if: 
all(x < y) || all(x < -y) || all(x < z) || all(x < -z)

    Does NOT project to -X viewport if: 
all(!(x < y)) || all(!(x < -y)) || all(!(x < z)) || all(!(x < -z))

    Does NOT project to +Y viewport if: 
all(!(x < y)) || all(x < -y) || all(!(z < y)) || all(z < -y)

    Does NOT project to -Y viewport if: 
all(x < y) || all(!(x < -y)) || all(z < y) || all(!(z < -y))

    Does NOT project to +Z viewport if: 
all(!(x < z)) || all(x < -z) || all(z < y) || all(z < -y)

    Does NOT project to -Z viewport if: 
all(x < z) || all(!(x < -z)) || all(!(z < y)) || all(!(z < -y))

These 6 expressions depend on 12 bits known as prim_plane_mask_0 (positive terms) and prim_plane_mask_1 (negative terms), in different combinations. Let?s rewrite them:

prim_plane_mask_0 = reverse {abcdef}, where
    a = all(x < y), b = all(x < -y), c = all(x < z), 
    d = all(x < -z), e = all(z < y), f = all(z < -y)

prim_plane_mask_1 = reverse {mnopqr}, where 
    m = all(!(x < y)), n = all(!(x < -y)), o = all(!(x < z)), 
    p = all(!(x < -z)), q = all(!(z < y)), r = all(!(z < -y))

    A bitwise function that selects x[i] if s[i] = 0, and selects y[i] otherwise
let bitselect(x,y,s) = x & ~s | y & s

    The _ symbol is just zero, used for aligning terms into the xy_xz_zy pattern.
    Does NOT project to +X viewport if: 
a || b || c || d || _ || _ = prim_plane_mask_0 & 0b1111 != 0

    Does NOT project to -X viewport if: 
m || n || o || p || _ || _ = prim_plane_mask_1 & 0b1111 != 0

    Does NOT project to +Y viewport if: 
m || b || _ || _ || q || f = bitselect(prim_plane_mask_0, prim_plane_mask_1, 0b01xx01) & 0b110011 != 0

    Does NOT project to -Y viewport if: 
a || n || _ || _ || e || r = bitselect(prim_plane_mask_0, prim_plane_mask_1, 0b10xx10) & 0b110011 != 0

    Does NOT project to +Z viewport if: 
_ || _ || o || d || e || f = bitselect(prim_plane_mask_0, prim_plane_mask_1, 0b0001xx) & 0b111100 != 0

    Does NOT project to -Z viewport if: 
_ || _ || c || p || q || r = bitselect(prim_plane_mask_0, prim_plane_mask_1, 0b1110xx) & 0b111100 != 0

These experssions can be efficiently calculated in this form, but we can optimize them further, get rid of the bitselect operations. Every expression simply selects a set of bits from prim_plane_mask_0 and prim_plane_mask_1 and tests whether all of them are zeros. We combine these 6-bit masks into one 16-bit word (for encoding convenience, prim_plane_mask_1 is aligned at 8 bit boundary) and select those bits directly from that word. The expressions convert as follows:

    Does NOT project to +X viewport if: 
combined_mask & 0b0000_0000_0000_1111 != 0 // 0x000f, abcd

    Does NOT project to -X viewport if: 
combined_mask & 0b0000_1111_0000_0000 != 0 // 0x0f00, mnop

    Does NOT project to +Y viewport if: 
combined_mask & 0b0001_0001_0010_0010 != 0 // 0x1122, bf | mq

    Does NOT project to -Y viewport if: 
combined_mask & 0b0010_0010_0001_0001 != 0 // 0x2211, ae | nr

    Does NOT project to +Z viewport if: 
combined_mask & 0b0000_0100_0011_1000 != 0 // 0x0438, def | o

    Does NOT project to -Z viewport if: 
combined_mask & 0b0011_1000_0000_0100 != 0 // 0x3804, c | pqr

To add the near clip planes to this algorithm, following extensions have to be made:

1. Compute 6 more flags for each vertex: X < ±1, Y < ±1, Z < ±1.
2. Extend the ?combined_mask? word with ANDs of these flags from the three vertices.
3. Add one ?1? bit into each of the bit fields used to compute the viewport mask bits. The location of that ?1? bit should correspond to the location of the appropriate near plane in the combined mask.

The sample implements near clip plane culling done like that.